64 匹马,8 赛道,找出最快的 4 匹最少要几次?
1. 故事起源
有 64 匹马, 8 条赛道,要找出最快的 4 匹马,最少要几次呢?

2. 初步思考
很多同学可能第一反应就是,这个问题肯定不简单,应该有一些技巧,但技巧是啥呢,又一时想不出来。
其实呢,先别想得太复杂了,比如我现在就问你一个问题,有没有可能存在有一匹不用跑? 答案当然是不行。
3. 分析
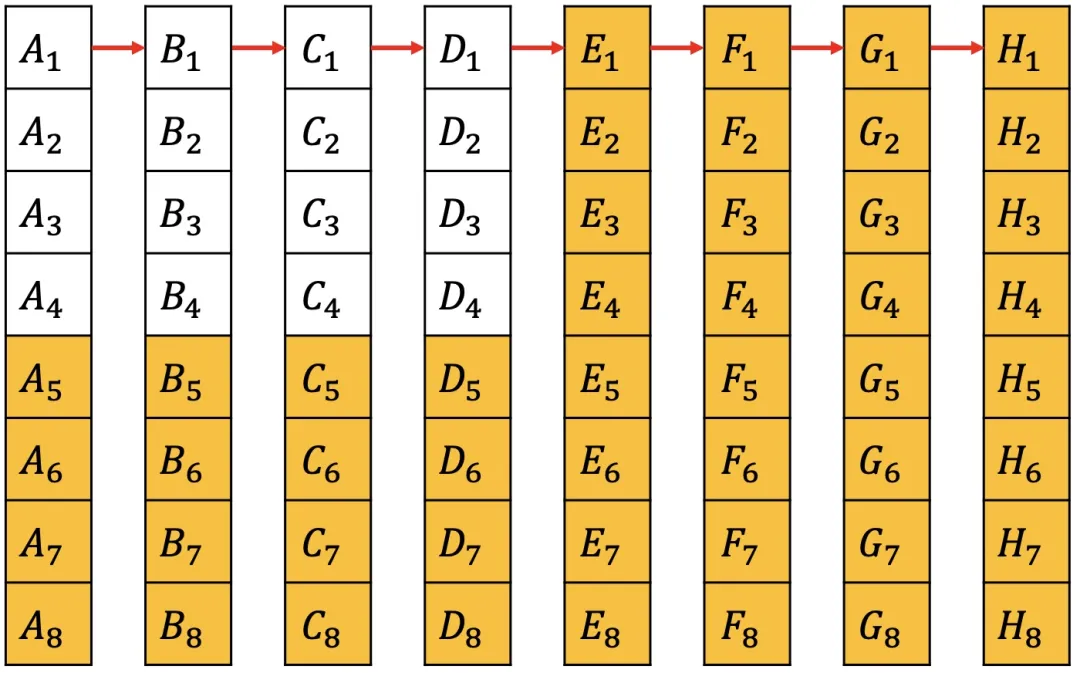
那也就是每一匹都得先跑一次, 64 匹, 8 个赛道,那就先分 8 组跑 8 次。
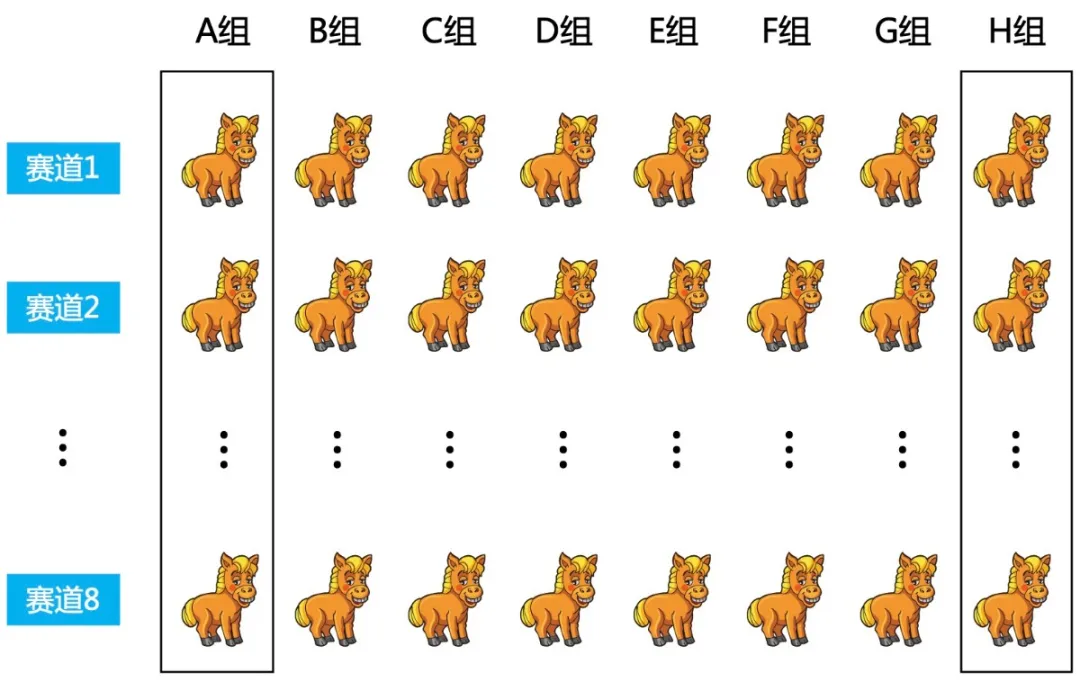
每一组都会得到 8 匹的相对速度,也就是在同一组内的名次。
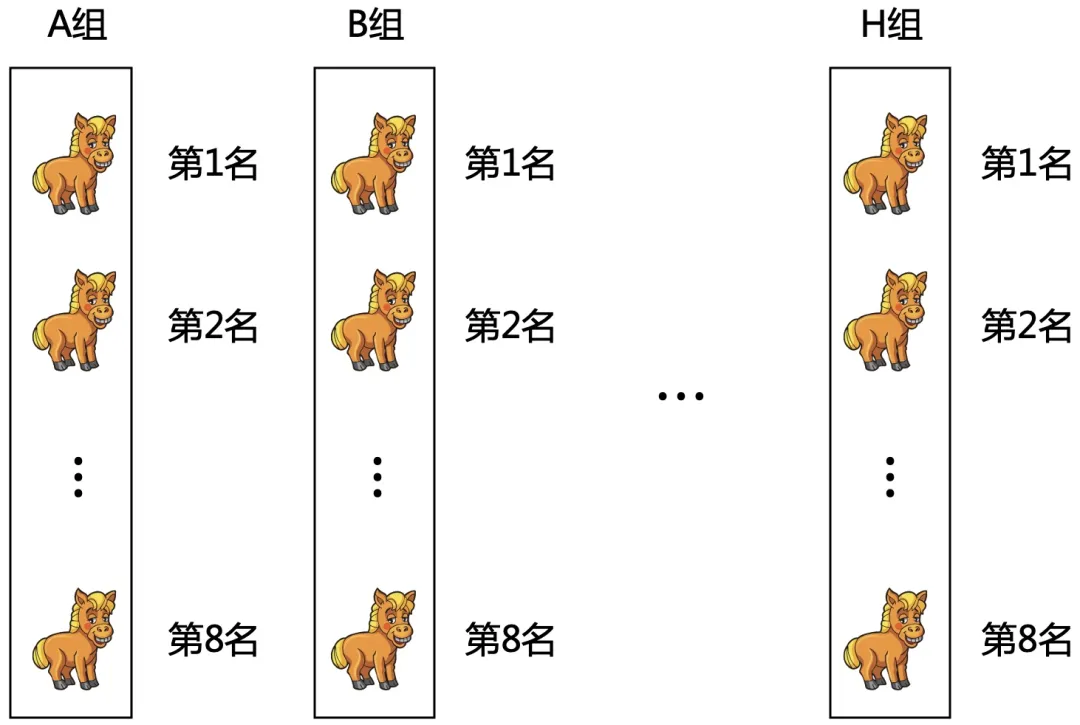
为了方便描述,我们用编号来表示。如 A 组里面的名次分别用 A~1~, A~2~, ..., A~8~ 来表示。

因为我们只需要找出最快的 4 匹,那么 A~5~, A~6~, A~7~, A~8~ 肯定不属于最快的 4 匹,同理把每一组的后 4 名先排除。
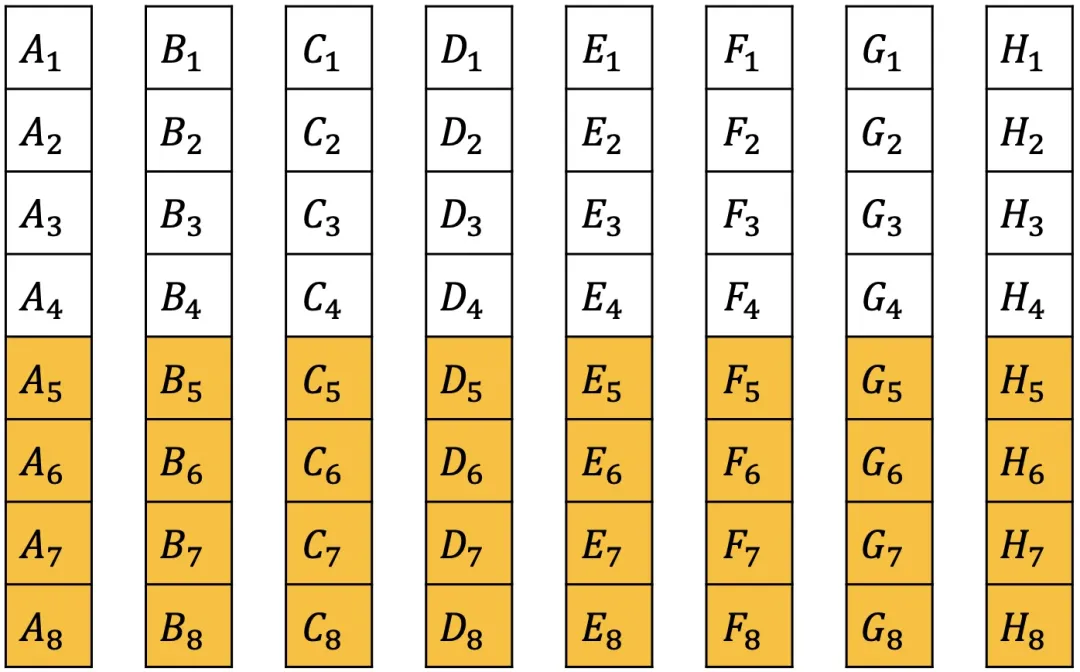
现在每一组内都有相对名次,但不同的组间是不知道的。如果把 A 组和 B 组放一起,下面的情况都可能存在。

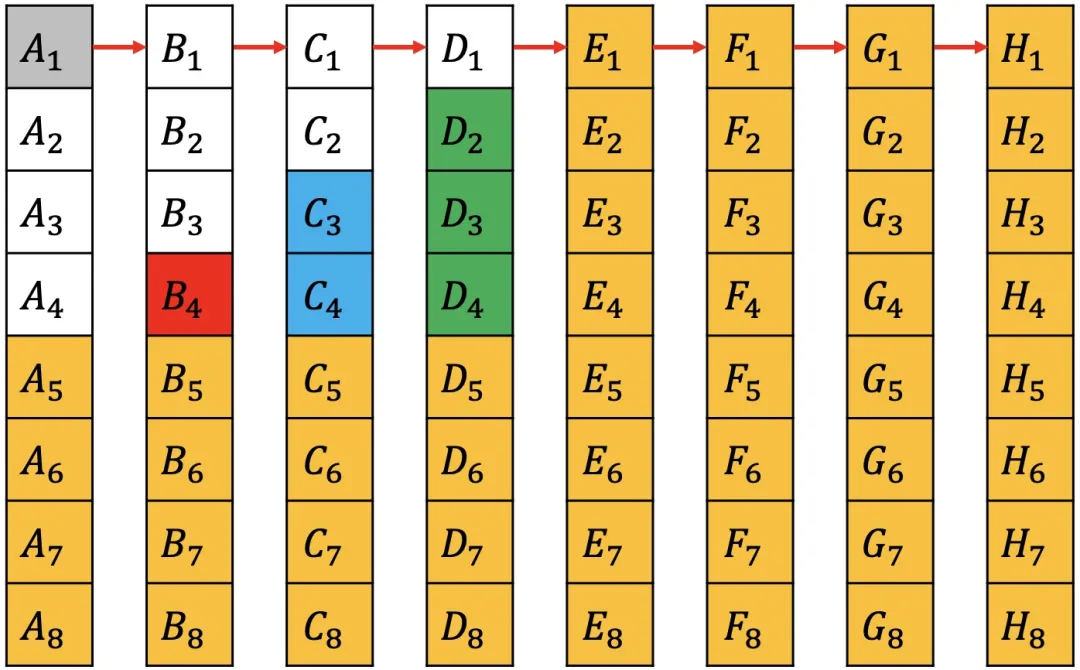
因为是要找最快的,所以选择每组的第一名再出来跑一次,这样落后的第一名所在的整组都可以排除。 为了描述方便,把最快到最慢的第一名所在的组依次重新命名为 A, B, ..., H 组。
组间的第一名有了名次关系,可以发现 D~2~, D~3~, D~4~ 一定不属于前 4 名,因为 A~1~, B~1~, C~1~, D~1~ 都在他们前面。 同理可排除 C~3~, C~4~, B~4~。同时 A~1~ 是最快的,一定属于前 4。 那接下来只需在剩下的 9 匹中找出前 3。
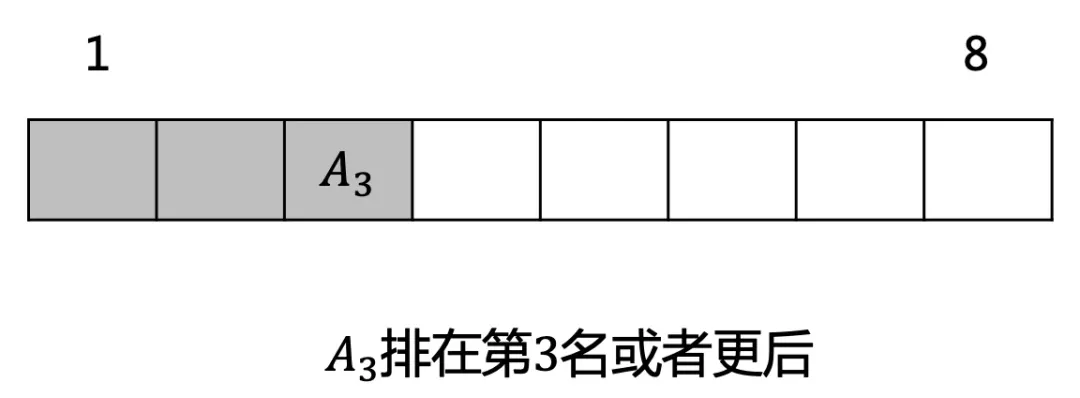
除去 A~4~, 其余 8 匹跑一次。如果 A~3~ 在第 3 名或者更后,那说明已经选出了前 3 名, A~4~ 也不用再跑了,否则再取前 3 和 A~4~ 一起跑一次,即可得结果。
最多 11 次一定可以选出最快的 4 匹。
4. 总结
这种思维题,其实是很难直接就想清楚整个过程。 可以先想得简单一点,往下推一步再看,逐步推进就可以引导出正确的结果了。