数据结构之 Heap 实现(TypeScript版)
Comparator实现见前文 前端比较方法的优雅封装。
1. 堆的定义
- 堆树是一颗完全二叉树;
- 堆树中某个节点的值总是不大于或不小于其子节点的值;
- 堆树中每个节点的子树都是堆树。
当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。如: 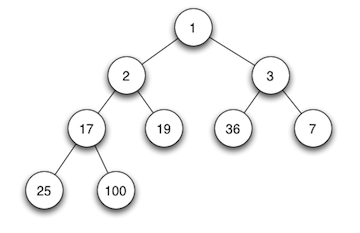
当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。如: 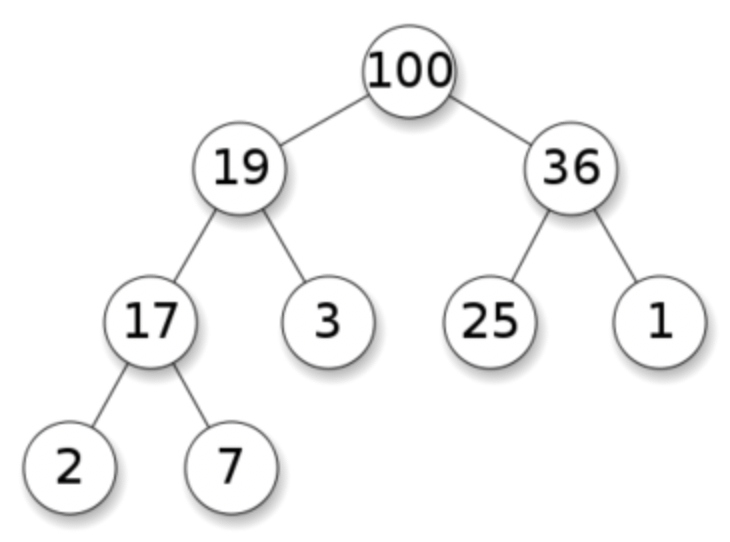
2. 实现思路
- 数据保存:数组保存堆节点信息,通过下标,可计算得出节点的父节点和左右子节点。
- 插入节点:先在堆的最后添加一个节点,然后沿着堆树上升。
- 删除节点:若为最后一个节点,则直接删除返回,否则将删除节点替换为最后一个节点,根据顺序情况决定堆树上升还是下降。
3. 代码实现
3.1 基本实现
ts
// data-structures/heap/MaxHeap.ts
import { TypeCompareParam } from '../../utils/comparator/Comparator';
import Heap from './Heap';
export default class MaxHeap extends Heap {
/**
* Checks if pair of heap elements is in correct order.
* For MinHeap the first element must be always smaller or equal.
* For MaxHeap the first element must be always bigger or equal.
*/
pairIsInCorrectOrder(firstElement: TypeCompareParam, secondElement: TypeCompareParam) {
return this.compare.greaterThanOrEqual(firstElement, secondElement);
}
}ts
// data-structures/heap/MinHeap.ts
import { TypeCompareParam } from '../../utils/comparator/Comparator';
import Heap from './Heap';
export default class MinHeap extends Heap {
/**
* Checks if pair of heap elements is in correct order.
* For MinHeap the first element must be always smaller or equal.
* For MaxHeap the first element must be always bigger or equal.
*/
pairIsInCorrectOrder(firstElement: TypeCompareParam, secondElement: TypeCompareParam) {
return this.compare.lessThanOrEqual(firstElement, secondElement);
}
}ts
// data-structures/heap/Heap.ts
import Comparator, { TypeCompareFun, TypeCompareParam } from '../../utils/comparator/Comparator';
/**
* Parent class for Min and Max Heaps.
*/
export default class Heap {
private heapContainer: TypeCompareParam[];
protected compare: Comparator;
/**
* @constructs Heap
*/
constructor(comparatorFunction?: TypeCompareFun) {
if (new.target === Heap) {
throw new TypeError('Cannot construct Heap instance directly');
}
// Array representation of the heap.
this.heapContainer = [];
this.compare = new Comparator(comparatorFunction);
}
/**
* 获取左子节点下标
*/
getLeftChildIndex(parentIndex: number) {
return 2 * parentIndex + 1;
}
/**
* 获取右子节点下标
*/
getRightChildIndex(parentIndex: number) {
return 2 * parentIndex + 2;
}
/**
* 获取父节点下标
*/
getParentIndex(childIndex: number) {
return Math.floor((childIndex - 1) / 2);
}
/**
* 判断是否有父节点
*/
hasParent(childIndex: number) {
return this.getParentIndex(childIndex) >= 0;
}
/**
* 判断是否有左子节点
*/
hasLeftChild(parentIndex: number) {
return this.getLeftChildIndex(parentIndex) < this.heapContainer.length;
}
/**
* 判断是否有右子节点
*/
hasRightChild(parentIndex: number) {
return this.getRightChildIndex(parentIndex) < this.heapContainer.length;
}
/**
* 获取左子节点
*/
leftChild(parentIndex: number) {
return this.heapContainer[this.getLeftChildIndex(parentIndex)];
}
/**
* 获取右子节点
*/
rightChild(parentIndex: number) {
return this.heapContainer[this.getRightChildIndex(parentIndex)];
}
/**
* 获取父节点
*/
parent(childIndex: number) {
return this.heapContainer[this.getParentIndex(childIndex)];
}
/**
* 根据下标交互数据
*/
swap(indexOne: number, indexTwo: number) {
const tmp = this.heapContainer[indexTwo];
this.heapContainer[indexTwo] = this.heapContainer[indexOne];
this.heapContainer[indexOne] = tmp;
}
/**
* 获取根节点
* 最小堆中对应最小值,最大堆中对应最大值
*/
peek() {
if (this.heapContainer.length === 0) {
return null;
}
return this.heapContainer[0];
}
/**
* 查找堆节点,返回对应的下标索引数组
*/
find(item: TypeCompareParam, comparator: Comparator = this.compare): number[] {
const foundItemIndices: number[] = [];
for (let itemIndex = 0; itemIndex < this.heapContainer.length; itemIndex += 1) {
if (comparator.equal(item, this.heapContainer[itemIndex])) {
foundItemIndices.push(itemIndex);
}
}
return foundItemIndices;
}
/**
* 判断堆是否为空
*/
isEmpty(): boolean {
return !this.heapContainer.length;
}
/**
* 将堆数据转为字符串展示
*/
toString() {
return this.heapContainer.toString();
}
/**
* Checks if pair of heap elements is in correct order.
* For MinHeap the first element must be always smaller or equal.
* For MaxHeap the first element must be always bigger or equal.
*/
/* istanbul ignore next */
pairIsInCorrectOrder(firstElement: TypeCompareParam, secondElement: TypeCompareParam): boolean {
throw new Error(`
You have to implement heap pair comparision method
for ${firstElement} and ${secondElement} values.
`);
}
}3.2 堆树上升
ts
// data-structures/heap/Heap.ts
// ...
export default class Heap {
// ...
/**
* 指定节点进行堆树上升
*/
heapifyUp(customStartIndex?: number) {
// Take the last element (last in array or the bottom left in a tree)
// in the heap container and lift it up until it is in the correct
// order with respect to its parent element.
let currentIndex = customStartIndex || this.heapContainer.length - 1;
while (
this.hasParent(currentIndex)
&& !this.pairIsInCorrectOrder(this.parent(currentIndex), this.heapContainer[currentIndex])
) {
this.swap(currentIndex, this.getParentIndex(currentIndex));
currentIndex = this.getParentIndex(currentIndex);
}
}
// ...
}3.3 堆树下降
ts
// data-structures/heap/Heap.ts
// ...
export default class Heap {
// ...
/**
* 指定节点进行堆树下降
*/
heapifyDown(customStartIndex = 0) {
// Compare the parent element to its children and swap parent with the appropriate
// child (smallest child for MinHeap, largest child for MaxHeap).
// Do the same for next children after swap.
let currentIndex = customStartIndex;
let nextIndex = null;
while (this.hasLeftChild(currentIndex)) {
if (
this.hasRightChild(currentIndex)
&& this.pairIsInCorrectOrder(this.rightChild(currentIndex), this.leftChild(currentIndex))
) {
nextIndex = this.getRightChildIndex(currentIndex);
}
else {
nextIndex = this.getLeftChildIndex(currentIndex);
}
if (this.pairIsInCorrectOrder(this.heapContainer[currentIndex], this.heapContainer[nextIndex])) {
break;
}
this.swap(currentIndex, nextIndex);
currentIndex = nextIndex;
}
}
// ...
}3.4 取出根节点
ts
// data-structures/heap/Heap.ts
// ...
export default class Heap {
// ...
/**
* 取出根节点
* 最小堆中对应最小值,最大堆中对应最大值
* 取出后,若还有节点,则将最后节点替换到当前根节点,然后进行堆树下降
*/
poll() {
if (this.heapContainer.length === 0) {
return null;
}
if (this.heapContainer.length === 1) {
return this.heapContainer.pop();
}
const item = this.heapContainer[0];
// Move the last element from the end to the head.
this.heapContainer[0] = this.heapContainer.pop();
this.heapifyDown();
return item;
}
// ...
}3.5 增加堆节点
ts
// data-structures/heap/Heap.ts
// ...
export default class Heap {
// ...
/**
* 增加一个堆节点
* 增加的堆节点在最右侧,所以只需要从最右侧进行堆树上升即可
*/
add(item: TypeCompareParam) {
this.heapContainer.push(item);
this.heapifyUp();
return this;
}
// ...
}3.6 删除堆节点
ts
// data-structures/heap/Heap.ts
// ...
export default class Heap {
// ...
/**
* 删除指定的堆节点
*/
remove(item: TypeCompareParam, comparator: Comparator = this.compare) {
// Find number of items to remove.
const numberOfItemsToRemove = this.find(item, comparator).length;
for (let iteration = 0; iteration < numberOfItemsToRemove; iteration += 1) {
// We need to find item index to remove each time after removal since
// indices are being changed after each heapify process.
const indexToRemove = this.find(item, comparator).pop();
// If we need to remove last child in the heap then just remove it.
// There is no need to heapify the heap afterwards.
if (indexToRemove === this.heapContainer.length - 1) {
this.heapContainer.pop();
}
else {
// Move last element in heap to the vacant (removed) position.
this.heapContainer[indexToRemove] = this.heapContainer.pop();
// Get parent.
const parentItem = this.parent(indexToRemove);
// If there is no parent or parent is in correct order with the node
// we're going to delete then heapify down. Otherwise heapify up.
if (
this.hasLeftChild(indexToRemove)
&& (!parentItem || this.pairIsInCorrectOrder(parentItem, this.heapContainer[indexToRemove]))
) {
this.heapifyDown(indexToRemove);
}
else {
this.heapifyUp(indexToRemove);
}
}
}
return this;
}
// ...
}